Blog

This blog is a continuing discussion among viewers and the author. Click here to send a question, a comment, or a response to a previous post.

The FFD model for processing information in the brain is new and apparently considered radical, so challenges and criticisms are especially welcome.

Lane 4/2/12

Very cool site. It is exactly the kind of site I was looking for before I started going back to school for my engineering degree when I was looking for sites about neural nets, synthetic biology, evolutionary programming, and robotics. This site would be very high on my list.

Bob 2/13/12

Hey, thanks. And the topics you were looking for would be good keywords for the site. We do have some common interests.

Lane 2/13/12

Dr. Yoder: Great website! Very informative, interesting, and even fun to explore. Why is the FFD model controversial?

Evan 4/2/12

Thanks for the comments, Evan.

It seems that the model is controversial largely because the claim that FFDs explain well-known brain phenomena is quite broad and detailed. The published papers show the circuits generate the main properties of color vision and olfaction. There is apparently no other explicit model that can explain even one of the phenomena.

The FFD model is also a radical departure from everything else that has been proposed to explain how the brain processes information. It's a hybrid theory that draws on concepts from several fields. That makes it difficult for any one person to fully understand all of it. For this reason, hybrid papers in general have a hard time getting published, let alone being accepted by the scientific community.

Lane Yoder 4/2/12

I saw your MARVELOUS website: astonishing! "Animations" are FANTASTIC! All seems easier to understand and appreciate than the paper.

Arturo 4/29/12

Thanks for the high praise.

Lane 5/1/12

This kind of approach to brain functioning is revolutionary: it no longer involves the "common" Boolean logic (like AI) or the simple "connections" among the parts of the brain (like connectionism and functionalism), but is able to explain our perceptions as well as, in the future, our sensations, common sense and reasoning.

Arturo 6/6/12

Several people have raised questions in private communications outside of the “Contact Us” link. I’ll comment on these questions here from time to time.

Question: I see how a how a decoder could identify the smell of a skunk with a single output “skunk” neuron if the skunk odorant stimulates some olfactory receptor types fully and others not at all. But how would the odorant be recognized by a fuzzy decoder if some receptors are partially stimulated?

Answer: Let’s first translate the question to color, both because color properties are more familiar and because color vision is simpler with only three photoreceptor types. The example diagram at the top of the website, repeated below, shows a greenish-yellow photostimulus that leaves all three photoreceptor types partially activated at different levels. Both the Green and Yellow output cells are activated, corresponding to our perception of both green and yellow. We may recognize the color as a combination of green and yellow, or we may give it a single name like "chartreuse." In any case we can identify the color, recall it later, and distinguish it from other color combinations such as greenish-blue. The skunk odorant may be similar. Partially stimulated olfactory receptors would produce a combination of FFD outputs, but we would recognize them as a distinctive perception.

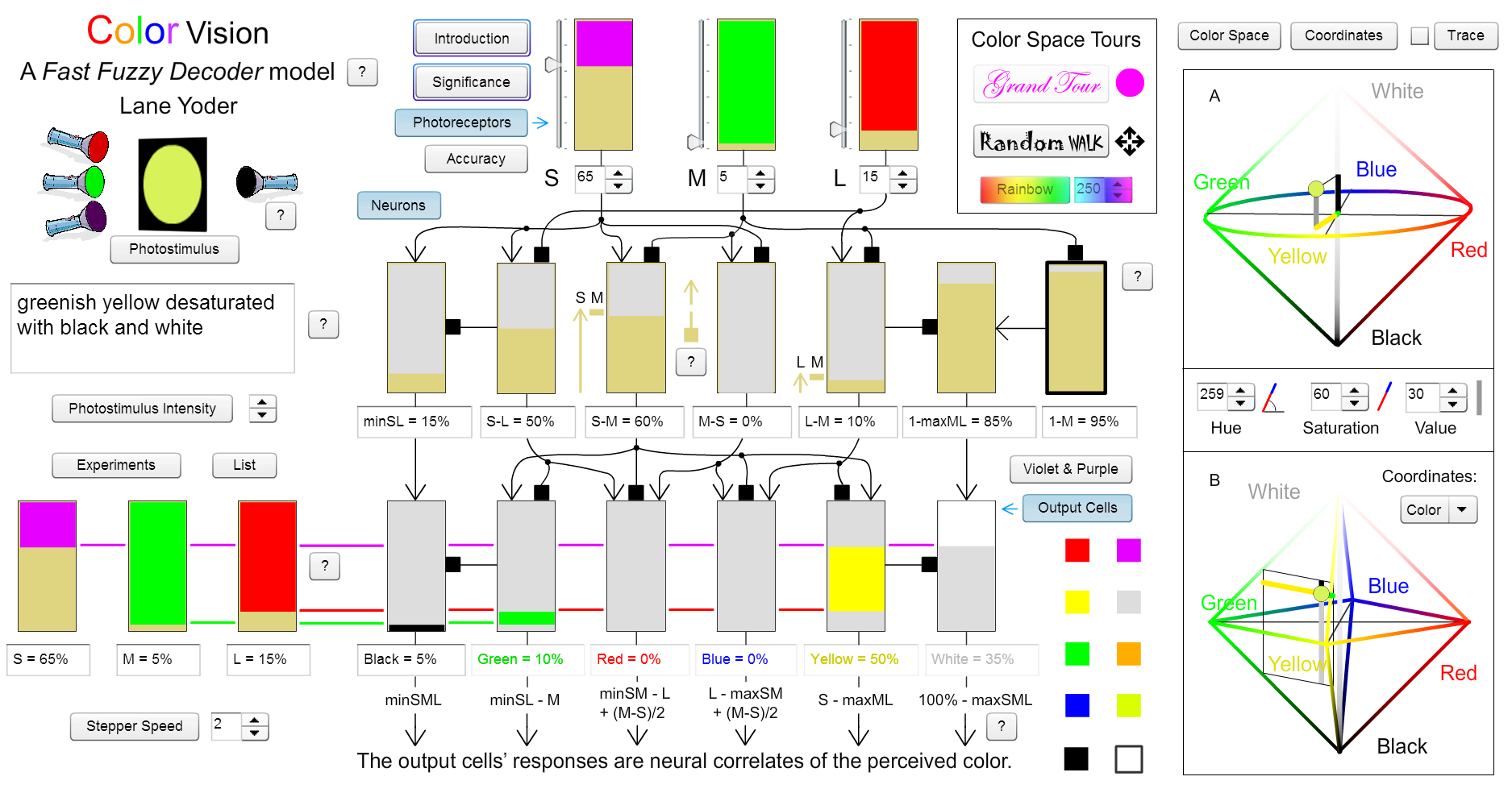
Be careful not to confuse stimuli with FFD outputs. An odorant consisting of a single type of molecule can activate several olfactory receptors at different levels, resulting in several FFD outputs, just as a photostimulus of a single wavelength can activate more than one photoreceptor type, resulting in more than one color cell output (e.g., see the greenish-yellow photostimulus in the interactive model's rainbow at 535 nm). On the other hand, a complex odorant consisting of many types of molecules might activate several olfactory receptors at the same level and the rest not at all, resulting in a single FFD output, just as a photostimulus with a broad power distribution can activate two photoreceptor types at one level and the third at a different level, resulting in a unique color (e.g., see the Yellow experiment in the Experiments button).

Lane 9/15/12

Question: What is the adaptive advantage in FFDs? If the skunk odor is identified by a combination of FFD outputs, why can’t it simply be identified by the combination of inputs from the olfactory receptors?

Answer: The combination of FFD output cells that have positive responses identifies the ordering of the strengths of the inputs independently of the strength of the stimulus (that is, independently of the concentration of an odorant or the intensity of a photostimulus). This combination informs the user (the individual with color vision or olfaction) of the chemical composition of an odorant or the spectral distribution of a photostimulus. A considerable amount of information can be expressed succinctly in the outputs: an FFD with n inputs can have 2ⁿ outputs, and at most n + 1 outputs can have positive responses simultaneously.

As a thought experiment in using the sensory inputs without further processing, suppose the three classes of photoreceptors produced red, green, and blue sensations directly. Since all photostimuli affect the activation of all photoreceptors to some extent, everything would appear to be combinations of red, green, and blue. Gleaning spectral information from these perceptions would be a difficult task. It might be possible to determine the blue component is stronger than the green component in some cases. But if their strengths are equal or nearly equal, the ordering would be difficult or impossible to determine consistently.

Lane 9/16/12

It is intriguing that your architectures seem to predict some of features of the brain. What I haven't understood from your Plos One paper is that your neurons have very small numbers of inputs and outputs, but real neurons have huge numbers. Why doesn't this undermine the applicability of the architectural conclusions?

Peter 11/14/12

Thanks for writing. Yes, the number of synaptic connections per neuron is a rather conspicuous difference between the FFD model and the brain.

Most of the FFDs’ neurons have fewer synaptic connections than are typical of actual neurons. This does not necessarily mean all networks in the brain operate fundamentally differently from FFDs. The FFDs show the simplest or nearly simplest ways neurons can be connected to function as decoders. For a variety of reasons, neurons in the brain may have more connections while performing the same functions in essentially the same ways. For example, the FFDs as shown do not have redundancies or other error-correcting mechanisms. These mechanisms alone could account for much of the massive connectivity of the brain. Another example is the convergence of inputs from several photoreceptors to a single second stage retinal cell both to limit the number of channels in the optic nerve and to ensure a signal is the result of photons rather than noise. In addition, cones and second stage neurons can provide input to different FFD color networks with overlapping receptive fields. Outputs of FFDs and other nano-networks may be useful as inputs to several networks in various parts of the brain. Shared inhibitory cells in FFDs have several connections. And there are probably more types of connections that don’t materially affect the way networks function but exist for reasons I’m not knowledgeable enough and clever enough to think of.

The purpose of FFDs is to show that logic circuits composed of neurons can perform known brain functions. Actual networks in the brain could be organized like these minimal networks in principle while being more elaborate in the details.

Lane 11/14/12

Question: How does the FFD model show that color space is shaped like two cones (Fig. A in the Interactive Model of Color Vision)?

Answer: This involves a little math, but the shape is due to the restriction on Color Space's cylindrical coordinates, r + |z| ≤ 1. This inequality follows the property that the sum of the Color Vision Model's outputs is 1 and from the definitions of r and z. (The sum equalling 1 depends on the linearity of the neurons' responses. In the simplified Interactive Model, they are assumed to be linear.) The coordinates r and z are defined in the first of the Related Articles and in Color Vision > Color Coordinates as r = Saturation = Red + Green + Blue + Yellow, and z = Value = White – Black.

So r + |z| = (Red + Green + Blue + Yellow) + |White - Black| ≤ Red + Green + Blue + Yellow + White + Black = 1.

Now since 0 ≤ r ≤ 1, the graph of r + |z| ≤ 1 looks like this:

The definition of the third cylidrical coordinate is θ = Hue = the angle of rotation of the color space point about the vertical axis. This angle has no restriction, so rotating the above graph about the z axis results in the double-cone shape of color space.

Lane 1/27/14

Question: How can neurons have fuzzy logic with signals that are spikes?

Answer: Neuron "spikes," or "all-or-nothing action potentials," are a source of much confusion, even among some neuroscientists. The all-or-nothing nature of the signal is often interpreted as implying the brain processes information digitally, that is, by encoding information in discrete signals like the zeros and ones of computers. The evidence seems to indicate that this is not the case. Many neurons, possibly most neurons, don't even generate action potentials. Instead they transmit "graded" potentials, signals of any magnitude within the physical limits of the neuron. The function of action potentials is evidently to transmit information reliably over long distances. This information is encoded mainly, if not entirely, in the frequency and duration of the train of action potentials. Frequency can be any number, again within the physical limits of the neuron. So action potentials convey information in graded signals, not discrete signals. If neurons don't use something like fuzzy logic to process information formatted in this way, something is missing in the brain's design.

Lane 2/11/14

Question: Why a decoder?

Answer: A decoder is absolutely necessary for color vision (as well as for olfaction). Color vision is, in fact, a decoder.

The color photoreceptors in the retina literally encode the photostimulus spectral information that we call color. Identifying the color from the combination of photoreceptor signals requires a decoder. You won't see this written anywhere except in the paper on color vision, even though it seems kind of obvious. The model in that paper is the only color vision model that is a decoder. And the only explicit model that produces neural correlates of color phenomena.

Here's a simplified version of the code and the decoded color. The three classes of color photoreceptors are sensitive to short, medium, and long wavelengths. Suppose three photoreceptors' signals S, M, and L have values of 1 or 0, depending on whether or not the corresponding photoreceptor is absorbing photons. The table below follows simply from an observation of the visible spectrum compared to the photoreceptors' sensitivity curves. (See the Rainbow Tour near the upper right of the Color Vision Model.)

Color vision associates a color with each combination of inputs from the three classes of photoreceptors.

Code #	Encoded spectral information SML	Decoded color
0	000	black
1	001	red
2	010	green
3	011	yellow
4	100	violet
5	101	purple
6	110	blue
7	111	white

Lane 5/2/18

Click here to send a question, a comment, or a response to a previous post.